Given a dataset consisting of m samples x each with 2 features ($x_1, x_2$) such that $x^{(i)} \in \mathbb{R}^2$.
These samples are classified into 2 classes $y^{(i)} \in {0,1}$.

We want to perform a binary classification using a neural network with a hidden layer consisting of 3 neurons such that:

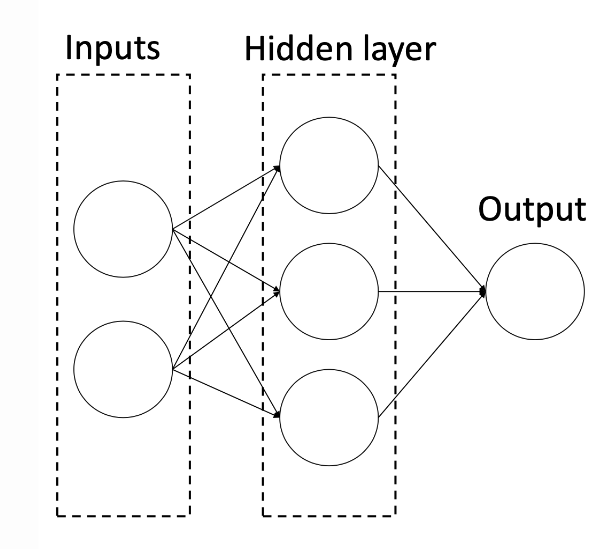
We denote the 3 neurons by ($a_1, a_2, a_3$) and define the corresponding logits ($\bar{a_1}, \bar{a_2}, \bar{a_3}$):

\[\bar{a_1} = w_{11}x_1 + w_{21}x_2 + w_{01}\] \[\bar{a_2} = w_{12}x_1 + w_{22}x_2 + w_{02}\] \[\bar{a_3} = w_{13}x_1 + w_{23}x_2 + w_{03}\]

We also define the logit corresponding to the output $\hat{y}$:

\[\bar{\hat{y}} = w_{1}a_1 + w_{2}a_2 + w_3 a_3 + w_{0}\]

We will use the average squared loss for the loss function:

\[L(y, \hat{y}) = \frac{1}{m}\sum_{i=1}^m (\hat{y}^{(i)} - y^{(i)})^2\]

---

a.

If we use the Sigmoid function as the activation function for ($a_1, a_2, a_3$) and $\hat{y}$, we apply $\sigma$ on the logits, getting:

\[a_1 = \sigma(w_{11}x_1 + w_{21}x_2 + w_{01})\] \[a_2 = \sigma(w_{12}x_1 + w_{22}x_2 + w_{02})\] \[a_3 = \sigma(w_{13}x_1 + w_{23}x_2 + w_{03})\] \[\hat{y} = \sigma(w_{1}a_1 + w_{2}a_2 + w_3 a_3 + w_{0})\] \[= \sigma\left( w_1 \sigma(w_{11}x_1 + w_{21}x_2 + w_{01}) + w_2 \sigma(w_{12}x_1 + w_{22}x_2 + w_{02}) + w_3 \sigma(w_{13}x_1 + w_{23}x_2 + w_{03}) + w_0\right)\]

Applying the gradient descent method, if we want to update the weight $w_{12}$ for a given learning rate $\eta$, we have to compute the gradient $\nabla_{w_{12}}$ of the loss function:

\[w_{12} \leftarrow w_{12} - \eta \nabla_{w_{12}}L(y, \hat{y})\]

Expressing the loss function as:

\[L(y, \hat{y}) = ||\hat{y} - y||^2\] \[= || \sigma\left( w_1 \sigma(w_{11}x_1 + w_{21}x_2 + w_{01}) + w_2 \sigma(w_{12}x_1 + w_{22}x_2 + w_{02}) + w_3 \sigma(w_{13}x_1 + w_{23}x_2 + w_{03}) + w_0\right) - y||^2\]

We will need to apply the chain rule multiple times to find $\nabla_{w_{12}}L(y, \hat{y})$.

Define:

\[A = w_1 \sigma(w_{11}x_1 + w_{21}x_2 + w_{01}) + w_2 \sigma(w_{12}x_1 + w_{22}x_2 + w_{02}) + w_3 \sigma(w_{13}x_1 + w_{23}x_2 + w_{03}) + w_0\] \[= w_1 \sigma(\bar{a_1}) + w_2 \sigma(\bar{a_2}) + w_3 \sigma(\bar{a_3})\]

The loss function can hence be written compactly as:

\[L(y, \hat{y}) = ||\sigma(A) - y||^2\]

Now, applying the chain rule step by step:

\[\frac{\partial L(y, \hat{y})}{\partial w_{12}} = 2\frac{\partial \sigma(A)}{\partial A}\frac{\partial A}{\partial w_{12}} (\sigma(A) - y)\] \[= 2\frac{\partial \sigma(A)}{\partial A} \left[ w_1 \frac{\partial \sigma(\bar{a_1})}{\partial w_{12}} + w_2 \frac{\partial \sigma(\bar{a_2})}{\partial w_{12}} + w_3\frac{\partial \sigma(\bar{a_3})}{\partial w_{12}}\right] (\sigma(A) - y)\]

But $\frac{\partial \sigma(\bar{a_1})}{\partial w_{12}}, \frac{\partial \sigma(\bar{a_3})}{\partial w_{12}} = 0$, hence:

\[\frac{\partial L(y, \hat{y})}{\partial w_{12}} = 2w_2\frac{\partial \sigma(A)}{\partial A} \frac{\partial \sigma(\bar{a_2})}{\partial w_{12}} (\sigma(A) - y)\] \[= 2 w_2 \frac{\partial \sigma(A)}{\partial A} \frac{\partial \sigma(\bar{a_2})}{\partial \bar{a_2}} \frac{\partial \bar{a_2}}{\partial w_{12}} (\sigma(A) - y)\] \[= 2 w_2 x_1 \frac{\partial \sigma(A)}{\partial A} \frac{\partial \sigma(\bar{a_2})}{\partial \bar{a_2}} (\sigma(A) - y)\] \[= 2 w_2 x_1 \sigma(A) \left( 1 - \sigma(A) \right) \sigma(\bar{a_2}) \left( 1 - \sigma(\bar{a_2})\right) (\sigma(A) - y)\] \[= 2w_2 x_1 \; \hat{y}(1-\hat{y})\;\sigma \big( w_{12}x_1 + w_{22}x_2 + w_{02}\big) \big(1 - \sigma\big( w_{12}x_1 + w_{22}x_2 + w_{02}\big) \big)\; (\hat{y} - y)\]

---

b.

We were given a scatter plot of the values of the output y being 0 or 1 given the values of ($x_1, x_2$).
The values of ($x_1, x_2$) in the input space are symbolized by × if y = 1 and by ○ if y = 0.

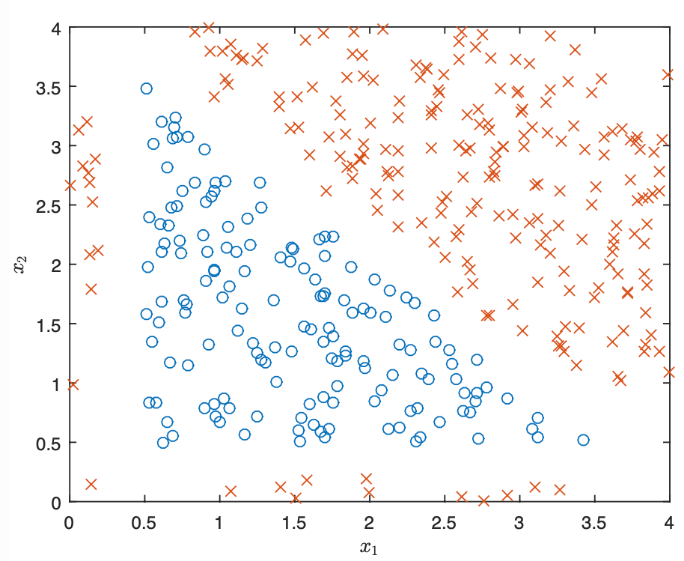
To classify this dataset with 100% accuracy, we need a model that produces a decision boundary that perfectly separates the two regions.

We are now working with a neural network with 1 hidden layer consisting of 3 neurons and with the activation functions all being the unit step function:

\[f(x) = \begin{cases} 1, & x \ge 0 \\ 0, & x < 0 \end{cases}\]

Our best option to achieve 100% accuracy is to let each neuron in the hidden layer determine one side of the decision boundary.
Looking at the above graph, we need 3 sides (a triangle) to form the best decision boundary.

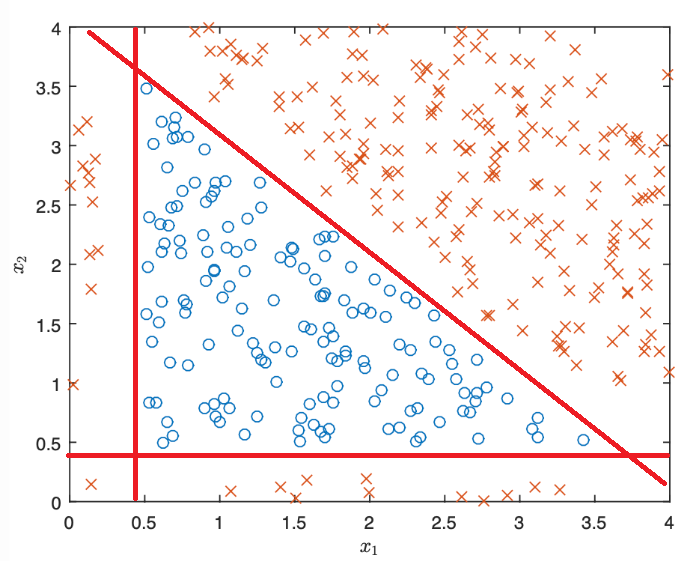
We want the activation function to return 0 when ($x_1, x_2$) lies within the triangle and 1 when it lies outside.

Each neuron independently:

• Neuron 1: $a_1 = f(\bar{a_1})$
  Vertical side: separates values of $x_1$ around 0.4.
  Set $\bar{a_1} = 0.4 - x_1$ → $f(\bar{a_1}) = 0$ for $x_1 > 0.4$, $f(\bar{a_1}) = 1$ for $x_1 \le 0.4$.

• Neuron 2: $a_2 = f(\bar{a_2})$
  Horizontal side: separates values of $x_2$ around 0.4.
  Set $\bar{a_2} = 0.4 - x_2$ → $f(\bar{a_2}) = 0$ for $x_2 > 0.4$, $f(\bar{a_2}) = 1$ for $x_2 \le 0.4$.

• Neuron 3: $a_3 = f(\bar{a_3})$
  Oblique side: intersects both axes at approximately 4.2.
  Set $\bar{a_3} = x_1 + x_2 - 4.2$.

Comparing with the general form $\bar{a_i} = w_{1i}x_1 + w_{2i}x_2 + w_{0i}$:

\[\bar{a_1} = -x_1 + 0.4 \\ \bar{a_2} = -x_2 + 0.4 \\ \bar{a_3} = x_1 + x_2 - 4.2\]

Hence:

\[w_{01} = 0.4, \; w_{11} = -1, \; w_{21} = 0, \; w_{02} = 0.4,\; w_{12} = 0,\; w_{22} = -1,\; w_{03} = -4.2,\; w_{13} = 1,\; w_{23} = 1\]

To get the predicted output $\hat{y}$, apply the step function:

\[\hat{y} = f(w_1 a_1 + w_2 a_2 + w_3 a_3 + w_0)\]

Set equal contributions for all neurons:

\[w_1 = w_2 = w_3 = 1\]

We determine $w_0$ as follows:
When all neurons return 0, we expect $\hat{y} = 0$, meaning $f(w_0) = 0$, so $w_0 < 0$.
If 2 neurons return 0 and 1 returns 1, we expect $\hat{y} = 1$, meaning $f(1 - w_0) = 1$, so $w_0 > -1$.
Hence we set:

\[w_0 = -1\]

---

c.

If we now set the activation functions for $a_1, a_2, a_3$ to be linear functions:

\[a_1 = w_{11}x_1 + w_{21}x_2 + w_{01}\] \[a_2 = w_{12}x_1 + w_{22}x_2 + w_{02}\] \[a_3 = w_{13}x_1 + w_{23}x_2 + w_{03}\]

and the step function for $\hat{y}$:

\[\hat{y} = f(A) = f(w_1 a_1 + w_2 a_2 + w_3 a_3 + w_0)\]

A 0 loss corresponds to perfect accuracy ($\hat{y} = y$).
We again assign each neuron to a side of the triangular decision boundary:

\[a_1 = 0.4 - x_1 \\ a_2 = 0.4 - x_2 \\ a_3 = x_1 + x_2 - 4.2\]

To reach 100% accuracy, we want $f(A) = 0$ when all ($a_1, a_2, a_3$) are strictly negative,
and $f(A) = 1$ when any of them is $\ge 0$.

Let all neurons be negative:

\[\hat{y} = f(w_1 \ominus_1 + w_2 \ominus_2 + w_3 \ominus_3 + w_0)\]

However, there is no set of weights $(w_0, w_1, w_2, w_3)$ ensuring $\hat{y} = 0$ for all negative parameters $(\ominus_1, \ominus_2, \ominus_3)$.
Hence, for this choice of activation functions, no specific set of weights will make the loss = 0.